O nosso 3º encontro da II etapa de formação, ocorrida no dia 26/04/2017, foi bastante movimentado e interativo.
Utilizamos como base para o nosso encontro a arte da dobradura. A nossa ideia com essa etapa da formação era apresentar a dobradura não só como uma estratégia pedagógica para o ensino de conteúdos matemáticos, mas, sobretudo, mostrar a relação entre arte, matemática e cultura, trabalhar elementos como organização, concentração, persistência, cuidado, atenção e respeito. Para tanto o encontro foi organizado em quatro etapas.
Na primeira etapa, ângulos, nos propomos apresentar os elementos básicos da geometria, como ponto/vértice, segmento/lado/diagonal, eixos de simetria, ângulos, dentre outros, fazendo uso de um quadrado de papel.
Iniciamos o trabalho com a construção de triângulos, fazendo uso de recursos nominais e demonstrativos dos referidos elementos da geometria. Daí, como resultante desta atividade, fizemos a demonstração de que, em qualquer triângulo, a soma de seus ângulos internos resulta em 180º.
Iniciando a segunda atividade com a construção de quadriláteros como retângulos, losangos, paralelogramos, quadrados e trapézios. Observou-se, pelas dobraduras, que os quadriláteros podiam ser constituídos de dois triângulos, e, partindo do conhecimento de que a soma dos ângulos internos de um triângulo é igual a 180º, ficou fácil concluir que, em qualquer quadrilátero, a soma dos ângulos internos é igual a 2 vezes 180º (referente aos dois triângulos), ou seja, 360º.
Ao construirmos um pentágono e um hexágono, os participantes chegaram a conclusão de que o número de triângulo que constitui as figuras estava em função do número dos seus respectivos lados, ou seja, o número de triângulos diferentes formados pelas diagonais de um vértice em comum dos polígonos era igual ao número de lados que o constituía, menos dois. Sabendo que soma dos ângulos internos de qualquer triângulo é igual 180, chegou-se a seguinte propriedade: S(n) = (n - 2) x 180.
Na segunda etapa, simetria, nos propomos a apresentar o conceito e os diferentes tipos de simetria. Conversamos sobre a presença da simetria na arte (a partir dos trabalhos de Maurits Cornelis Escher) e na natureza (com uso de diferentes tipos de imagens).
Circle Limit IV (1960).
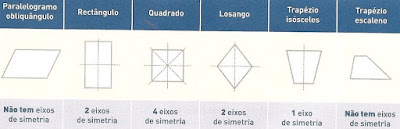
Na sequência, por meio do trabalho com dobradura, apresentamos os eixos simétricos nos diferentes tipos de triângulos e quadriláteros.
Na terceira etapa, foi trabalhada a construção de parábolas. Para essa atividade, os professores do NAEH construíram em um recorte de papel recebido um segmento de reta s qualquer e um ponto F, externo à reta. Sobre o segmento, foi proposto que construíssem um número sugestivo de pontos superior a sete (como parâmetro), sendo estes denominados, conforme sequência, de A, B, C..., G...
Dobrando a folha de papel, um a um, de formando vincos em cada etapa, cada ponto da reta deveria se unir ao ponto F fazendo um vinco visível de segmento perpassando de A a F, de B a F e assim por diante. Por fim, conforme se pode ver na figura seguinte, a tarefa era finalizada com a construção da parábola.
Essa atividade foi enriquecida com informações e propriedades da parábola e seus respectivos elementos como Foco, vértice, pontos máximos e mínimos, eixo de simetria, dentre outros.
A quarta e última etapa do encontro foi bastante especial, no sentido de que apresentamos um pouco da arte e cultura milenar japonesa denominada de Origami. conversamos sobre os diferentes usos de papéis, bem como das tradições, crenças e lendas por trás das figuras e formas. Nessa etapa foi essencial auxiliar os presentes a fazer leitura dos diagramas (seja no modelo brasileiro ou japonês).
Após ficarem curiosos em conhecer as magias que circundam o pássaro, iniciamos a construção do Tsuru, uma figura mística e recheada de desafios no seu processo de construção. Os resultados e a satisfação dos participantes podem ser conferidos nas fotos seguintes.
Segue o diagrama para a construção do Tsuru:
Como desenvolvimento de atividades envolvendo o Origami, segue o link para a apostila "Oficina de histórias contadas com origamis", de Irene Tanabi.
Como desenvolvimento de atividades envolvendo o Origami, segue o link para a apostila "Oficina de histórias contadas com origamis", de Irene Tanabi.